数学四上第五单元试卷一参考答案
1.A
【分析】从平行四边形的一条边上任意一点都可以向对边作垂直线段,即是平行四边的高。据此解答。
【详解】平行四边形的每一条边都可以看成是底,所以平行四边形有4条底,有无数条高。
答案:A
【点评】考查平行四边形的高的定义及画法。
2.C
【分析】同一平面内,相交成直角的两条直线互相垂直,两条互相垂直的直线相交的夹角都是直角;据此即可解答。
【详解】两条直线相交成直角,则形成的四个角均是直角。
答案:C
【点评】考查了学生同一平面内两条直线位置关系的知识;用到的知识点:互相垂直的含义。
3.D
【分析】在同一平面内,由不在同一条直线上的四条线段首尾顺次相连组成的封闭图形,叫做四边形。长方形、正方形、平行四边形、梯形都属于四边形,正方形是特殊的长方形,长方形和正方形都是特殊的平行四边形;梯形和平行四边形是不同的两种四边形,据此分析。
【详解】如图 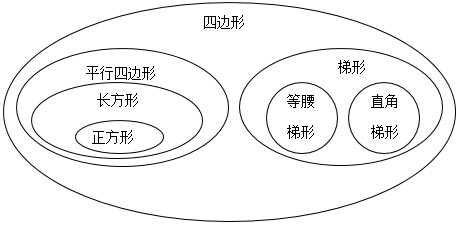 ,题干图中A表示的图形是梯形。
,题干图中A表示的图形是梯形。
答案:D
【点评】关键是熟悉各种四边形特征,掌握四边形的分类。
4.C
【分析】两条直线相交成直角时,这两条直线互相垂直,其中一条直线是另一条直线的垂线,这两条直线的交点叫做垂足。据此解答。
【详解】互相垂直的是线段AD和DC。
答案:C
【点评】考查垂直的特征,要求哪两条线段互相垂直,关键是找出哪两条线段的夹角是直角。
5.D
【分析】根据三角形、平行四边形、长方形和梯形的意义和特征进行判断即可。
【详解】A.三角形有三条边首尾顺次相连,重叠部分的图形有4条边,故不是三角形;
B.平行四边形有两组互相平行的对边,重叠部分的图形只有一组对边平行,故不是平行四边形。
C.长方形有四个直角,重叠部分的图形没有直角,故不是长方形;
D.梯形有一组对边平行,一组对边不平行,重叠部分的图形符合梯形的特征,故为梯形。
【点评】解决的关键是熟练掌握三角形、平行四边形、长方形和梯形的特征。
6.C
【分析】观察图形可知,单独上面一层有6个梯形,单独下面一层有4个梯形,上、下层合起来有4个梯形,据此解题即可。
【详解】6+4+4=14(个)
所以,图中一共有14个梯形。
答案:C
【点评】认真观察图形,有序数出图中梯形的个数,是解答此题的关键。
7.B
【分析】端点在两条平行线上且垂直于平行线的线段,这些线段延长后永无交点,这些线段是互相平行的。
【详解】与两条平行线垂直的所有线段互相平行。
答案:B
【点评】在同一平面内,永不相交的两条直线互相平行。
8.B
【分析】因为正方形拉成平行四边形后四条边的长度不变,则正方形的周长就不会发生变化,所以这个平行四边形的周长等于正方形的周长,根据正方形的周长=边长×4,据此解答。
【详解】4×4=16(厘米)
这个平行四边形的周长是16厘米。
答案:B
【点评】解答此题的关键是明白:正方形拉成平行四边形后四条边的长度不变。
9.线段AC
【分析】主要考查点到直线的距离:连接直线外一点与直线上各点的所有线段中,垂线段最短,这条垂线段的长度,叫做点到直线的距离。
【详解】图中,线段AB,AC,AD,AE中,因为线段AC⊥BE,所以最短的一条线段是线段AC。
【点评】解决的关键是明确从直线外一点到这条直线的线段中,垂直线段最短。而这个性质常用于解决求最短路线的问题。
10.③⑤ ②⑥
【分析】根据平行线和互相垂直的定义:在同一平面内,不相交的两条直线叫做平行线;在同一平面内,当两条直线相交成90度时,这两条直线互相垂直;据此进行解答。
【详解】互相垂直的有③⑤,互相平行的有②⑥。
【点评】此题考查了平行和垂直的定义,注意基础知识的积累。
11.互相平行
【分析】根据垂直和平行的特征:同一平面内两条直线都垂直于同一条直线,那么这两条直线互相平行;进而解答即可。
【详解】如果两条直线都垂直于同一条直线,那么这两条直线互相平行。
【点评】此题考查了垂直和平行的特征及性质。
12.垂直线段
【分析】从直线外一点向直线可以作无数条线段,其中垂直线段最短。如图分析观察:
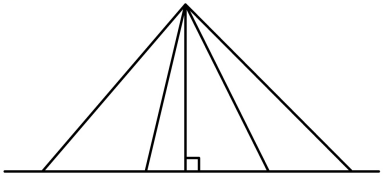
【详解】过直线外一点向直线作的垂直线段最短。
【点评】考查了垂线的性质。
13.互相垂直 a⊥b##b⊥a
【分析】两条直线相交成直角时,这两条直线互相垂直,其中一条直线是另一条直线的垂线,这两条直线的交点叫做垂足。
【详解】如图,直线a和直线b的位置关系是(互相垂直),记作(a⊥b)
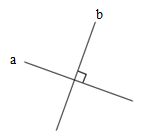
【点评】熟悉垂直的定义是解答此题的关键。
14.3
【分析】同一平面内不相交的两条直线互相平行,其中一条直线是另一条直线的平行线。据此解答即可。
【详解】图中有3组互相平行的线段。
【点评】学生根据平行的特征能够正确判断出图中平行线的组数是解决的关键。
15.2##两
【分析】利用画图直观的看一看,在同一平面内,画与已知直线相距2厘米的平行线有2条,在已知直线的两边各有1条。
【详解】如图所示:
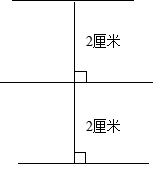
在同一平面内画与已知直线相距2厘米的平行线可以画2条。
【点评】考查了平行线的知识,结合题意,画出图示,是解答此题的关键。
16.无数 1##一
【分析】在同一平面内,和一条直线平行的直线可以画无数条;过直线外一点,作已知直线的垂线,点到直线的垂直线段只有一条,据此解答。
【详解】在同一平面内,与已知直线平行的直线有无数条,过直线外一点作已知直线的垂线,可以作1条。
【点评】考查了垂直与平行的性质。
17.√
【分析】连接直线外一点与直线各点的所有线段中,垂线段最短,据此解答。
【详解】过直线外一点向已知直线画垂线,只能画一条。
答案:√
【点评】熟练掌握垂线段的定义并灵活应用是解答此题的关键。
18.√
【分析】同一平面内,永不相交的两条直线互相平行,相交成直角的两条直线互相垂直。
【详解】教室门的两条长边互相平行,相交的两条边互相垂直。
答案:√
【点评】熟练掌握平行和垂直的特征是解答此题的关键。
19.√
【分析】单个的平行四边形3个,两个小平行四边形组成的有2个,三个小平行四边形组成的有1个。再相加即可解答。
【详解】3+2+1=6(个)
答案:√
【点评】平行四边形的两组对边分别平行且相等,先判断单个的平行四边形,再判断组合而成的平行四边形,然后判断总数即可
20.×
【详解】平行四边形的概念:两组对边分别平行的四边形;它的特征是两组对边分别相等,两组对角也分别相等。一个平行四边形,它的对边相等,对角也相等,不是四个角相等,故原题干说法错误。
答案:×
21.见详解
【分析】(注意:直线两端可以无限延长)
在同一平面内,如果两条直线只有一个公共点,则这两条直线相交;
在同一平面内,如果两条直线没有公共点,则这两条直线平行;
如果两条直线相交,且所成的角为直角,则这两条直线互相垂直。
根据相交、平行、垂直的定义由图依次进行判断并连线。
【详解】由相交、平行、垂直的定义可知,
图中第一行的第三个、第二行的第二个属于两直线垂直;
第一行的第一个、第三个及第二行的第二个、第三个属于两直线相交;
第一行的第二个、第二行的第一个属于两直线平行。
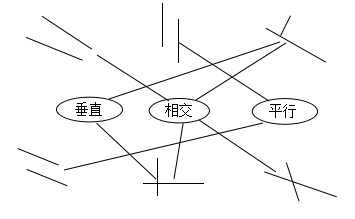
【点评】主要考查了对判断平面内两直线位置关系知识的掌握与理解。
22.见详解
【分析】画图方法:把三角板的一条直角边与已知直线重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线重合的直角边和A点重合,过A点沿三角板的直角边画直线即可。
【详解】 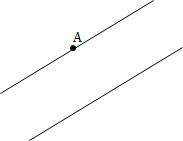
【点评】考查平行线的作法,培养作图能力。
23.见详解
【分析】(1)连接两点的线段的长度叫做两点间的距离。两点之间线段最短。据此可知,要找到从蘑菇房到小木屋最近的路,只需要将蘑菇房和小木屋用线段连接起来即可。
(2)从直线外一点到这条直线的线段中,垂直线段最短,这条垂直线段的长度叫做点到直线的距离。据此可知,要找到从蘑菇房通向小河最近的路,则从蘑菇房向小河作垂线,这条垂线即为所求。
【详解】 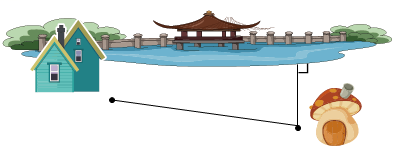
【点评】考查线段和垂直的性质。两点之间线段最短。从直线外一点到这条直线的线段中,垂直线段最短。
24.见详解
【分析】三角形是由同一平面内不在同一直线上的三条线段首尾顺次连接所组成的封闭图形;只有一组对边平行的四边形是梯形。
【详解】(1) 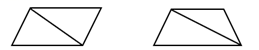
(2) 
(3) ![]()
(答案不唯一)
【点评】熟练掌握三角形以及梯形的定义是解答此题的关键。
25.见详解
【分析】在同一平面内,当两条直线相交成90度(即直角)时,这两条直线互相垂直;据此进行解答。
【详解】根据垂直的定义:因为门框的角是直角,所以门框是垂直的。
【点评】此题考查了垂直的定义,注意基础知识的积累。
26.B方案;加装的木板与椅子组成了一个三角形。三角形具有稳定性,可使椅子更稳定。
【分析】三角形具有稳定性,四边形具有易变形的特点,据此解答即可。
【详解】B方案比较好。理由:在B方案中,加装的木板与椅子组成了一个三角形。三角形具有稳定性,可使椅子更稳定。
【点评】熟悉三角形具有稳定性、四边形易变形的特点是解答此题的关键。
27.24米
【分析】求护栏的长度,即是求该梯形花坛的周长,梯形的周长等于上底、下底及两腰的长度之和,据此列式计算即可解答。
【详解】4+10+5+5
=14+5+5
=19+5
=24(米)
答:护栏长24米。
【点评】解答理解周长的含义,了解等腰梯形的特点,从而解决问题。
28.(1)图见详解过程
(2)平行
(3)我认为李明会获胜,根据比赛规则,最好的一次成绩作为最终的成绩,张军的最好成绩是410厘米,李明虽然跳了两次,但其中一次的成绩为420厘米,比张军的最好成绩要好,所以我认为李明会获胜(答案不唯一)
【分析】(1)把踏跳板看作一条直线,跳到的位置看作一个点,画出点到直线的距离,就是两次跳远的距离;
(2)根据在同一平面内,同时垂直于同一条直线的两条直线互相平行,可知所画的两条线段互相平行;
(3)答案不唯一,结合李明和张军跳远的成绩进行解答即可。
【详解】(1)两次跳远的距离如图所示:
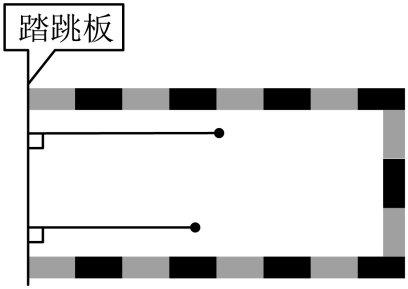
(2)所画的两条线段互相平行。
(3)我认为李明会获胜,根据比赛规则,最好的一次成绩作为最终的成绩,张军的最好成绩是410厘米,李明虽然跳了两次,但其中一次的成绩为420厘米,比张军的最好成绩要好,所以我认为李明会获胜。(答案不唯一)
【点评】主要考查点到直线的距离、垂直以及平行的定义在实际生活中的应用。